Parameter tuning for a Residual Deep Image-to-Image CNN ←
This network design has the following features:
- simple and repetitive, makes programmer's life less troublesome
- supports any image size (above a certain threshold): put one image in, get the same size out
- supports the all-famous deep-ness, e.g. the training gradient does not vanish after a lot of layers - and we all believe that many layers are good
Since this is a logbook, i might as well write down how the idea came along. I was working like a mad person on a new CLIPig implementation, using OpenAI's CLIP network to massage a mess of pixels into something matching a text prompt and looking good. There are much cooler things out there, my personal favorite being Stable Diffusion, but none of them can be put on my graphics card. So to wrap it short, i'm developing image generation tools that run on a, nowadays, average graphics card with 6 GB of VRAM. For artistic reasons, i was interested in some form of noise reduction to make the rendered images look more pleasing and started with this simple design.
While network trainings were running, i searched through
arxiv.org for image de-noising, quickly limiting
results to before 2017, because i really don't understand all this
Diffusion stuff and its all high computational effort.
Found this paper: "Generalized Deep Image to Image Regression" which describes a recursive branching design and subsequently made a little implementation. It works quite nice but is mostly too slow for my taste, also i don't like the max-pooling layers for generative networks. After some playing around with it i came back to the simpler CNNs but remembered a few of the ideas and ways of thinking from the above and other papers.
Now that i have written most of the content below, i make a pause and will read Image Restoration Using Convolutional Auto-encoders with Symmetric Skip Connections which seems to do the exact thing.
--
This simple CNN is composed of an encoder and a decoder, while the decoder is the reverse of the encoder. The layout is (in pytorch style):
ResConv(
(encoder): ModuleDict(
(layer_1): ConvLayer(
(bn): BatchNorm2d(1, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv): Conv2d(1, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(act): GELU(approximate='none')
)
(layer_...): ConvLayer(
(bn): BatchNorm2d(32, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv): Conv2d(32, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(act): GELU(approximate='none')
)
)
(decoder): ModuleDict(
(layer_...): ConvLayer(
(bn): BatchNorm2d(32, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv): ConvTranspose2d(32, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(act): GELU(approximate='none')
)
(layer_15): ConvLayer(
(bn): BatchNorm2d(32, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv): ConvTranspose2d(32, 1, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(act): Sigmoid()
)
)
)
In the forward pass each encoder layer stores it's result which is later
added to the input of the inverse decoder layer. In the example above, result
of layer_1 is added to the output of layer_14 which is the input of layer_15.
I think this is basically a U-NET. In any case, we can add as much layers as we want, while still being able to train the network. The residual connections will propagate the gradients through the whole thing, while demanding tasks will utilize the deeper layers because they have a larger receptive field. For a little discussion of the receptive field, please check Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising (Zhang et al).
All experiments, unless noted otherwise,
- do 3 epochs (3 runs through the 60,000 training images)
-
use
AdamWoptimizer- with default deltas 0.9, 0.999
- learn rate of 0.0003
- use
CosineAnnealingLRscheduler (that decreases learn rate to zero using a 1/4 cosine curve over the full run) - a mini batch size of 64
- use Mean Absolute Error (l1) between output and target image as the loss function (The l2 or Mean Squared Error loss is much more common but i personally find the l1 numbers more readable)
To evaluate the abilities of the network, it's trained to restore the deleted top, bottom, left or right half of an image. In this case, zalando's beloved Fashion-MNIST dataset, scaled to 32x32 pixels (without interpolation).
It's not completely ridiculous to expect the network to make up a complete half since the images are all nicely centered and contain more or less the same stuff (shirts, jackets, shoes, bags...).
Here are two examples (from the worst (first image) and the best network of the following experiment). Odd rows show the network input and even rows the reconstruction from the network.
| worst | best |
|---|---|
 |
 |
The first network only has one layer (one convolution and one de-convolution), so it's receptive field is only 3x3 pixels (that of the one convolutional kernel). It is therefore not able to generate the other half of the image.
Compare number of layers ←
Comparing the performance of the number of layers.
experiment file: experiments/denoise/resconv-test.yml @ 1a748720...
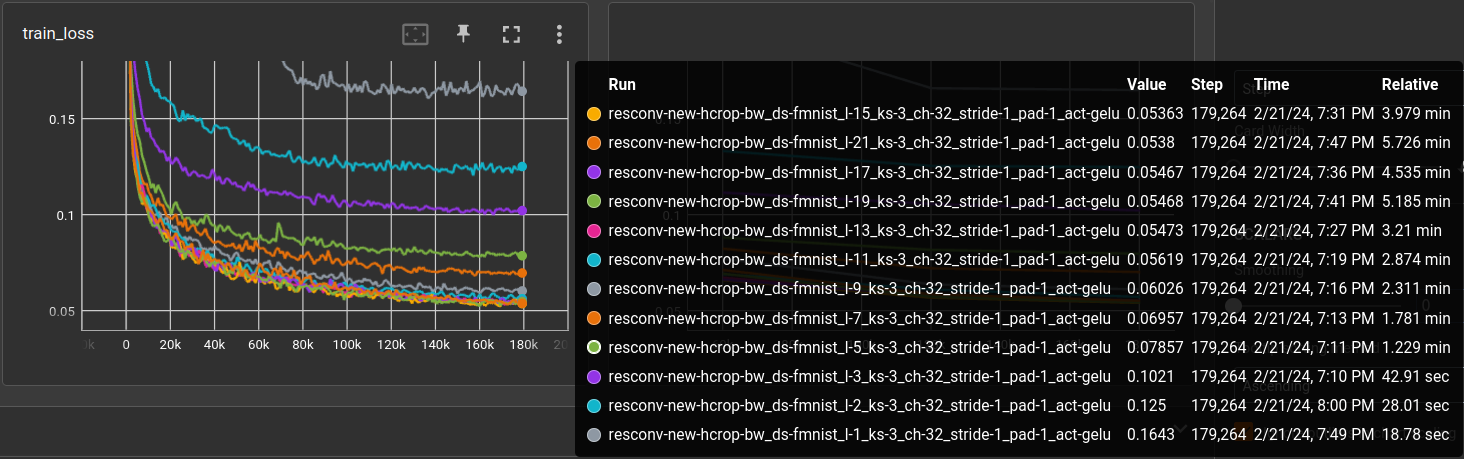
| layers | ks | ch | stride | pad | act | validation loss | model params | train time (minutes) |
|---|---|---|---|---|---|---|---|---|
| 15 | 3 | 32 | 1 | 1 | gelu | 0.054141 | 261,411 | 4.17 |
| 19 | 3 | 32 | 1 | 1 | gelu | 0.054439 | 335,907 | 5.43 |
| 13 | 3 | 32 | 1 | 1 | gelu | 0.054911 | 224,163 | 3.39 |
| 21 | 3 | 32 | 1 | 1 | gelu | 0.055190 | 373,155 | 5.98 |
| 17 | 3 | 32 | 1 | 1 | gelu | 0.055413 | 298,659 | 4.74 |
| 11 | 3 | 32 | 1 | 1 | gelu | 0.057229 | 186,915 | 3.02 |
| 9 | 3 | 32 | 1 | 1 | gelu | 0.061094 | 149,667 | 2.43 |
| 7 | 3 | 32 | 1 | 1 | gelu | 0.070167 | 112,419 | 1.87 |
| 5 | 3 | 32 | 1 | 1 | gelu | 0.079709 | 75,171 | 1.30 |
| 3 | 3 | 32 | 1 | 1 | gelu | 0.102242 | 37,923 | 0.78 |
| 2 | 3 | 32 | 1 | 1 | gelu | 0.124805 | 19,299 | 0.52 |
| 1 | 3 | 32 | 1 | 1 | gelu | 0.164834 | 675 | 0.36 |
It's really nice to see such a distinguished parameter-performance scaling, once in a while. From 1 to 11 layers, performance increases steadily, then it get's a bit mixed-up. Most likely, 11 layers archive a receptive field that includes the whole input patch of 32x32. It's kind of proving that the deep layers are used despite the residual skip connections.
I'm not very patient in these regards, but i ran the same experiment on
64x64 images. Note that the computation time is drastically increased.
Because of the padding of 1, each layer processes a full 64x64 block on
32 channels.
| layer | ks | ch | stride | pad | act | validation loss | model params | train time (minutes) |
|---|---|---|---|---|---|---|---|---|
| 21 | 3 | 32 | 1 | 1 | gelu | 0.0610384 | 373,155 | 25.13 |
| 30 | 3 | 32 | 1 | 1 | gelu | 0.0646240 | 540,771 | 35.27 |
| 17 | 3 | 32 | 1 | 1 | gelu | 0.0652571 | 298,659 | 19.57 |
| 19 | 3 | 32 | 1 | 1 | gelu | 0.0661678 | 335,907 | 19.95 |
| 15 | 3 | 32 | 1 | 1 | gelu | 0.0694179 | 261,411 | 17.27 |
| 13 | 3 | 32 | 1 | 1 | gelu | 0.0728544 | 224,163 | 22.02 |
| 11 | 3 | 32 | 1 | 1 | gelu | 0.0752024 | 186,915 | 18.75 |
| 9 | 3 | 32 | 1 | 1 | gelu | 0.0809892 | 149,667 | 15.87 |
| 7 | 3 | 32 | 1 | 1 | gelu | 0.0889331 | 112,419 | 11.31 |
| 5 | 3 | 32 | 1 | 1 | gelu | 0.1045170 | 75,171 | 7.49 |
| 3 | 3 | 32 | 1 | 1 | gelu | 0.1328610 | 37,923 | 3.79 |
| 1 | 3 | 32 | 1 | 1 | gelu | 0.1641830 | 675 | 0.47 |
The steady increase in precision per extra layer is a bit better than with the 32x32 images, although it's not much.
Note that the 21-layer network has about the same validation loss as the 9-layer network for 32x32 images. Another provy incidence that the number of layers directly relates to the receptive field size. The 3x3 kernel CNN needs about 20 layers to see an area of about 40x40 pixels.
However, the 30 layer network does not improve performance. I'm currently unable to explain that. It could be related to the residual weight factor of 0.1 that i used up until the next experiment.
Anyway, it's actually quite interesting how a network with only a few hundred thousand parameters can be so slow. And memory hungry. And my laptop is starting to burn through my lap. The 30 layer version runs with less than a 100 inputs/sec, which is just terrible to bear (Not only because i'm inpatient but also because the task is purely academic and the input images are scaled from 28x28 to 64x64, so it's a waste of computation). Also the batch size needed to be reduced for 21 and 30 layer network training to make it fit in my available 6GB GPU RAM.
For comparing the following parameters i will use the 11 layer network on the original FMNIST resolution of 28x28 pixels:
Compare residual weight factor ←
Should one scale the residual signal that comes from the encoder layers
before adding it to the decoder layer input? It's denoted RWF in the
following expression and experimental results.
dec-layer input N = dec-layer output N-1 + RWF * enc-layer-output -N
| l | RWF | ks | ch | stride | pad | act | validation loss | model params | train time (minutes) |
|---|---|---|---|---|---|---|---|---|---|
| 11 | 1.00 | 3 | 32 | 1 | 1 | gelu | 0.0537689 | 186,915 | 2.38 |
| 11 | 0.50 | 3 | 32 | 1 | 1 | gelu | 0.0539687 | 186,915 | 2.33 |
| 11 | 2.00 | 3 | 32 | 1 | 1 | gelu | 0.0557501 | 186,915 | 2.38 |
| 11 | 0.05 | 3 | 32 | 1 | 1 | gelu | 0.0560915 | 186,915 | 2.26 |
| 11 | 0.10 | 3 | 32 | 1 | 1 | gelu | 0.0568670 | 186,915 | 2.29 |
| 11 | 0.01 | 3 | 32 | 1 | 1 | gelu | 0.0595923 | 186,915 | 2.13 |
It seems like: no, don't do it. Just keep it at 1.0.
Compare position of batch normalization? ←
In each layer, the batch norm was placed at the first position, more out of my intuition than actual knowledge.
ConvLayer( (bn): BatchNorm2d(1, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) (conv): Conv2d(1, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (act): GELU(approximate='none') )
It could be placed as well after the convolution:
ConvLayer( (conv): Conv2d(1, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (bn): BatchNorm2d(32, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) (act): GELU(approximate='none') )
or after the activation function
ConvLayer( (conv): Conv2d(1, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (act): GELU(approximate='none') (bn): BatchNorm2d(32, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) )
The following table lists the results for the different
batch-norm positions (bnp), separately for encoder (bnp-e)
and decoder (bnp-d).
0is before convolution1is after convolution2is after the activation-means no batch normalization
| l | ks | ch | stride | pad | act | bnp-e | bnp-d | validation loss | model params | train time (minutes) |
|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 3 | 32 | 1 | 1 | gelu | 0 | 0 | 0.0509118 | 186,787 | 2.07 |
| 11 | 3 | 32 | 1 | 1 | gelu | 0 | 1 | 0.0509330 | 186,787 | 2.22 |
| 11 | 3 | 32 | 1 | 1 | gelu | 1 | 0 | 0.0523070 | 186,849 | 2.31 |
| 11 | 3 | 32 | 1 | 1 | gelu | 1 | 1 | 0.0524035 | 186,849 | 2.32 |
| 11 | 3 | 32 | 1 | 1 | gelu | 0 | 2 | 0.0533116 | 186,787 | 2.25 |
| 11 | 3 | 32 | 1 | 1 | gelu | 1 | 2 | 0.0537457 | 186,849 | 2.32 |
| 11 | 3 | 32 | 1 | 1 | gelu | 2 | 1 | 0.0544390 | 186,849 | 2.33 |
| 11 | 3 | 32 | 1 | 1 | gelu | - | 0 | 0.0547576 | 186,209 | 2.22 |
| 11 | 3 | 32 | 1 | 1 | gelu | 2 | 2 | 0.0548645 | 186,849 | 2.33 |
| 11 | 3 | 32 | 1 | 1 | gelu | - | 1 | 0.0550985 | 186,209 | 2.21 |
| 11 | 3 | 32 | 1 | 1 | gelu | 2 | 0 | 0.0552446 | 186,849 | 2.33 |
| 11 | 3 | 32 | 1 | 1 | gelu | 0 | - | 0.0559730 | 186,147 | 2.17 |
| 11 | 3 | 32 | 1 | 1 | gelu | 1 | - | 0.0576676 | 186,209 | 2.22 |
| 11 | 3 | 32 | 1 | 1 | gelu | 2 | - | 0.0577886 | 186,209 | 2.22 |
| 11 | 3 | 32 | 1 | 1 | gelu | - | 2 | 0.0587750 | 186,209 | 2.21 |
| 11 | 3 | 32 | 1 | 1 | gelu | - | - | 0.1163260 | 185,569 | 2.10 |
Note that the best validation loss is actually better than in previous runs. After some tests, not shown here, the batch normalization was removed from the final encoder and decoder layers.
Compare activation function ←
Let's take all the good parts from before and compare the standard
activation functions available in pytorch.
However, the final decoder layer is always using the Sigmoid activation
because everybody knows it's a good activation for generating images
(everything is scaled to [0, 1] range).
| l | ks | ch | stride | pad | act | validation loss | model params | train time (minutes) |
|---|---|---|---|---|---|---|---|---|
| 11 | 3 | 32 | 1 | 1 | Mish | 0.0512072 | 186,787 | 2.52 |
| 11 | 3 | 32 | 1 | 1 | GELU | 0.0512259 | 186,787 | 2.29 |
| 11 | 3 | 32 | 1 | 1 | SiLU | 0.0514479 | 186,787 | 2.46 |
| 11 | 3 | 32 | 1 | 1 | Hardswish | 0.0515750 | 186,787 | 2.42 |
| 11 | 3 | 32 | 1 | 1 | LeakyReLU | 0.0522968 | 186,787 | 2.36 |
| 11 | 3 | 32 | 1 | 1 | ReLU6 | 0.0524871 | 186,787 | 2.42 |
| 11 | 3 | 32 | 1 | 1 | ReLU | 0.0530411 | 186,787 | 2.42 |
| 11 | 3 | 32 | 1 | 1 | PReLU | 0.0533523 | 186,807 | 2.59 |
| 11 | 3 | 32 | 1 | 1 | Softplus | 0.0544980 | 186,787 | 2.42 |
| 11 | 3 | 32 | 1 | 1 | LogSigmoid | 0.0547575 | 186,787 | 2.54 |
| 11 | 3 | 32 | 1 | 1 | CELU | 0.0551080 | 186,787 | 2.10 |
| 11 | 3 | 32 | 1 | 1 | Tanh | 0.0562118 | 186,787 | 2.36 |
| 11 | 3 | 32 | 1 | 1 | RReLU | 0.0566449 | 186,787 | 2.45 |
| 11 | 3 | 32 | 1 | 1 | Hardtanh | 0.0570635 | 186,787 | 2.47 |
| 11 | 3 | 32 | 1 | 1 | Softsign | 0.0571498 | 186,787 | 2.95 |
| 11 | 3 | 32 | 1 | 1 | SELU | 0.0601167 | 186,787 | 2.47 |
| 11 | 3 | 32 | 1 | 1 | Sigmoid | 0.0610033 | 186,787 | 2.44 |
| 11 | 3 | 32 | 1 | 1 | Hardsigmoid | 0.0647689 | 186,787 | 2.43 |
| 11 | 3 | 32 | 1 | 1 | Softshrink | 0.0805768 | 186,787 | 2.34 |
| 11 | 3 | 32 | 1 | 1 | Hardshrink | 0.0974769 | 186,787 | 2.24 |
| 11 | 3 | 32 | 1 | 1 | Tanhshrink | 0.1122510 | 186,787 | 2.60 |
Sometimes i wonder why there are so many activation functions when most of the time, the same ones perform best. Anyway, this result is slightly different to my MNIST classification results but as usual, you are good to choose either GELU, one of the ReLU variants or, as it turns out, the MISH activation.
Compare channel size ←
Currently all hidden convolutions have had 32 channels. In this experiment, i will test 16, 32, 64 and 128 channels, but also vary the channel size along the 11 layers.
For example ch1 = 16 and ch2 = 128 means, the encoder uses 16
channels for the first layer and linearly increases the number to
128 for the final layer. The decoder always has the reverse channel count,
to make the skip connections fit.
| l | ks | ch1 | ch2 | stride | pad | act | validation loss | model params | train time (minutes) |
|---|---|---|---|---|---|---|---|---|---|
| 11 | 3 | 128 | 128 | 1 | 1 | gelu | 0.0443586 | 2,958,979 | 10.66 |
| 11 | 3 | 128 | 64 | 1 | 1 | gelu | 0.0443985 | 1,712,091 | 8.83 |
| 11 | 3 | 128 | 32 | 1 | 1 | gelu | 0.0448816 | 1,280,341 | 7.01 |
| 11 | 3 | 128 | 16 | 1 | 1 | gelu | 0.0449165 | 1,109,285 | 6.30 |
| 11 | 3 | 64 | 128 | 1 | 1 | gelu | 0.0450236 | 1,710,773 | 8.64 |
| 11 | 3 | 64 | 64 | 1 | 1 | gelu | 0.0459730 | 742,211 | 4.15 |
| 11 | 3 | 32 | 128 | 1 | 1 | gelu | 0.0469918 | 1,278,363 | 7.08 |
| 11 | 3 | 16 | 128 | 1 | 1 | gelu | 0.0483264 | 1,106,979 | 6.40 |
| 11 | 3 | 64 | 32 | 1 | 1 | gelu | 0.0485725 | 426,357 | 3.48 |
| 11 | 3 | 64 | 16 | 1 | 1 | gelu | 0.0487565 | 319,347 | 3.03 |
| 11 | 3 | 32 | 64 | 1 | 1 | gelu | 0.0488293 | 425,699 | 3.62 |
| 11 | 3 | 32 | 32 | 1 | 1 | gelu | 0.0512699 | 186,787 | 2.48 |
| 11 | 3 | 16 | 64 | 1 | 1 | gelu | 0.0515703 | 318,357 | 3.03 |
| 11 | 3 | 32 | 16 | 1 | 1 | gelu | 0.0539735 | 105,925 | 2.06 |
| 11 | 3 | 16 | 32 | 1 | 1 | gelu | 0.0546895 | 105,595 | 1.88 |
| 11 | 3 | 16 | 16 | 1 | 1 | gelu | 0.0587657 | 47,315 | 1.39 |
What can be learned from it?
- more channels (at least up until 64) improve performance (without considering the computational cost).
- increased channel count is more important for the first shallow layers than the later deep layers
- the difference in archived training loss between 64 and 128 channels is at the 4th digit after the comma, so not really worth considering given the extra amount of required compute.
Compare kernel size ←
Out of old-fashionedness only odd kernel sizes are considered. For a fair comparison, the padding is adjusted to the individual kernel sizes such that each layer still processes the same spatial block (28x28).
| l | ks | ch | stride | pad | act | validation loss | model params | train time (minutes) |
|---|---|---|---|---|---|---|---|---|
| 11 | 5 | 32 | 1 | 2 | gelu | 0.0466142 | 515,491 | 2.10 |
| 11 | 7 | 32 | 1 | 3 | gelu | 0.0468494 | 1,008,547 | 5.12 |
| 11 | 9 | 32 | 1 | 4 | gelu | 0.0486901 | 1,665,955 | 7.29 |
| 11 | 11 | 32 | 1 | 5 | gelu | 0.0501364 | 2,487,715 | 9.44 |
| 11 | 3 | 32 | 1 | 1 | gelu | 0.0513643 | 186,787 | 2.16 |
Wow, there is a significant perfomance jump from 3 to 5, and the 5x5 kernel seems to run equally or even faster on my hardware/lib/driver setup. It is very likely, though, that the performance of the kernel size must be re-evaluated for each particular task.
Similar to the channel size abve , the kernel size is varied layer-wise in the following experiment.
The top performing network with ks1=3 and ks2=9, for example, has the following kernel sizes:
[3, 3, 5, 5, 5, 7, 7, 7, 7, 9, 9]
| l | ks1 | ks2 | ch | stride | act | validation loss | model params | train time (minutes) |
|---|---|---|---|---|---|---|---|---|
| 11 | 3 | 9 | 32 | 1 | gelu | 0.0434004 | 907,683 | 4.37 |
| 11 | 3 | 11 | 32 | 1 | gelu | 0.0435886 | 1,251,747 | 5.57 |
| 11 | 3 | 7 | 32 | 1 | gelu | 0.0449416 | 596,387 | 3.02 |
| 11 | 5 | 9 | 32 | 1 | gelu | 0.0454906 | 1,105,315 | 5.33 |
| 11 | 5 | 7 | 32 | 1 | gelu | 0.0461697 | 810,403 | 4.09 |
| 11 | 3 | 5 | 32 | 1 | gelu | 0.0462298 | 383,395 | 2.15 |
| 11 | 5 | 11 | 32 | 1 | gelu | 0.0462772 | 1,514,915 | 6.67 |
| 11 | 5 | 5 | 32 | 1 | gelu | 0.0467664 | 515,491 | 2.19 |
| 11 | 7 | 7 | 32 | 1 | gelu | 0.0469873 | 1,008,547 | 5.43 |
| 11 | 7 | 9 | 32 | 1 | gelu | 0.0474498 | 1,401,763 | 6.58 |
| 11 | 7 | 5 | 32 | 1 | gelu | 0.0478909 | 762,787 | 3.79 |
| 11 | 7 | 11 | 32 | 1 | gelu | 0.0482104 | 1,778,595 | 7.66 |
| 11 | 7 | 3 | 32 | 1 | gelu | 0.0482650 | 517,027 | 2.97 |
| 11 | 9 | 9 | 32 | 1 | gelu | 0.0483184 | 1,665,955 | 7.72 |
| 11 | 9 | 3 | 32 | 1 | gelu | 0.0486722 | 764,835 | 4.13 |
| 11 | 5 | 3 | 32 | 1 | gelu | 0.0486834 | 351,651 | 2.35 |
| 11 | 9 | 5 | 32 | 1 | gelu | 0.0487206 | 994,211 | 4.92 |
| 11 | 9 | 7 | 32 | 1 | gelu | 0.0488068 | 1,338,275 | 6.61 |
| 11 | 9 | 11 | 32 | 1 | gelu | 0.0488103 | 2,157,475 | 8.94 |
| 11 | 11 | 11 | 32 | 1 | gelu | 0.0495152 | 2,487,715 | 9.59 |
| 11 | 11 | 7 | 32 | 1 | gelu | 0.0497081 | 1,635,747 | 7.20 |
| 11 | 11 | 5 | 32 | 1 | gelu | 0.0499655 | 1,324,451 | 6.13 |
| 11 | 11 | 3 | 32 | 1 | gelu | 0.0499719 | 1,029,539 | 5.21 |
| 11 | 11 | 9 | 32 | 1 | gelu | 0.0500542 | 2,078,115 | 8.58 |
| 11 | 3 | 3 | 32 | 1 | gelu | 0.0512497 | 186,787 | 2.11 |
Wow, our little 3x3 kernel friend, that was used all the time, has the worst performance again. Also the 5x5 from the above experiment is surpassed. Generally, one can see: Small kernel size in shallow layers and larger kernel size in deeper layers is a good thing.
TODO:
-
compare
- conv groups