How does receptive field size increase with self-attention ←
Still not tired of these Very Small Language Models... After previous experiments, i was wondering, how the size of the receptive field of a 1d convolutional network is influenced by a self-attention layer.
Basically, the self-attention gives the network the opportunity to relate distant cells with each other that are (spatially or temporally) far more apart than the classic receptive field of the convolution can handle.
I tried a couple of new synthetic datasets but came back to the Selective Copying problem because it's quite simple to understand and to setup with a specific size.
Small recap: Selective copying means to pick all the letters in between those spaces and concatenate them:
A B C D : ABCD EG B A : EGBA
It's a simple task but requires a large-enough receptive field. I'm using the same text-to-text network as in previous experiments, masking out the answer and requiring the network to reproduce the whole string while replacing the mask with the actual answer (the concatenated letters).
The network gets the raw byte classes (256) as input and outputs class logits for each output character.
Each sample of the dataset contains 10 letters to concatenate in a 40 (or 80) wide space, denoted
as area in the table below. The network has 3 layers and either
uses a kernel size of 7 and dilation 1, 1, 1, which results in a receptive field radius of 9

or a kernel size of 13 and dilation 5, 7, 1, which results in a receptive field radius of 78

The table shows runs for various combinations of kernel-size/dilation, convolutional channels
and self-attention (attn) for a selective copying area of 40 and 80 cells. The attention
is the QK-self-invented type as described here.
| area | l | ch | ks | dil | attn | validation loss | validation mask error % | validation sample error% | model params | train time (minutes) | throughput |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 40 | 3 | 32 | 7 | 0.428964 | 88.9958 | 100 | 29,920 | 5.98 | 10,867/s | ||
| 40 | 3 | 32 | 7 | 0,T,T | 0.364131 | 72.3721 | 100 | 44,320 | 6.99 | 9,302/s | |
| 80 | 3 | 128 | 7 | 0,0,T | 0.108775 | 45.9375 | 99.9104 | 492,544 | 12.59 | 5,162/s | |
| 80 | 3 | 32 | 13 | 5,7,1 | 0.139426 | 46.3525 | 99.8308 | 48,352 | 16.95 | 3,834/s | |
| 40 | 3 | 32 | 13 | 5,7,1 | 0.147143 | 24.7432 | 92.2472 | 48,352 | 7.23 | 8,984/s | |
| 40 | 3 | 32 | 7 | 0,0,T | 0.060434 | 13.9844 | 82.0064 | 37,120 | 6.22 | 10,457/s | |
| 40 | 3 | 64 | 7 | 0,0,T | 0.037878 | 9.0555 | 64.6994 | 131,584 | 15.77 | 4,122/s | |
| 40 | 3 | 128 | 7 | 0,0,T | 0.024103 | 6.2549 | 48.0842 | 492,544 | 9.22 | 7,051/s | |
| 40 | 3 | 256 | 7 | 0,0,T | 0.019787 | 5.0681 | 39.8637 | 1,902,592 | 19.93 | 3,260/s | |
| 40 | 3 | 512 | 7 | 0,0,T | 0.019062 | 4.6715 | 37.5547 | 7,475,200 | 45.6 | 1,425/s | |
| 80 | 3 | 128 | 13 | 5,7,1 | 0,0,T | 8.94742e-07 | 0.0009 | 0.0099 | 885,760 | 17.85 | 3,641/s |
| 80 | 3 | 32 | 13 | 5,7,1 | 0,0,T | 3.31051e-06 | 0 | 0 | 61,696 | 24.17 | 2,689/s |
| 40 | 3 | 32 | 13 | 5,7,1 | 0,0,T | 1.91189e-06 | 0 | 0 | 61,696 | 8.72 | 7,454/s |
| 80 | 3 | 64 | 13 | 5,7,1 | 0,0,T | 4.2523e-07 | 0 | 0 | 229,888 | 10.02 | 6,489/s |
| 40 | 3 | 64 | 13 | 5,7,1 | 0,0,T | 4.06063e-07 | 0 | 0 | 229,888 | 7.97 | 8,153/s |
| 40 | 3 | 128 | 13 | 5,7,1 | 0,0,T | 4.15227e-08 | 0 | 0 | 885,760 | 12.63 | 5,144/s |
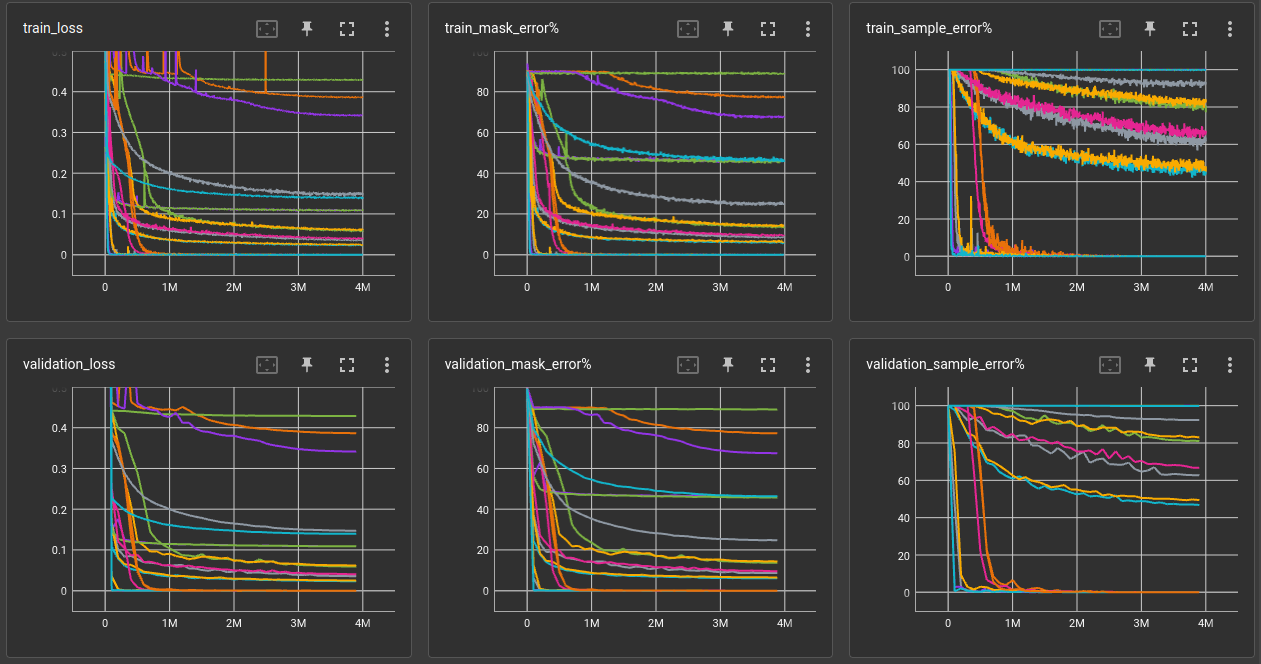
Looking at the validation sample error % we can see that neither a large receptive field nor
self-attention alone can solve the problem with a 3-layer network. Combining both, however, solves
the problem 100%.
Using only self-attention, the number of channels has a significant impact, although not as much as to justify the increased computational demand. All networks with attention where run two times and the average is reported. The 512-channel version had a validation error of 31.4% and 43.6%.